简单排序

冒泡排序

排序原理：

1、比较相邻的元素，如果前一个元素比后一个元素大，就交换这两个元素的位置

2、对每一对元素都这样处理，最后的出来的结构就是排序完成的结果

image-20220116195027877

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class BubbleTest{
    public static void main(String[] args) {
        //integer实现了comparable接口，提供了比较的规则
        Integer[] arr = {4,5,6,3,2,1};
        Bubble.sort(arr);
    }
}

public class Bubble {
    //对数组a中的元素进行排序
    public static void sort(Comparable[] a){
        for (int i=a.length-1;i>0;i--){
            for (int j=0;j<i;j++){
                //比较索引j和索引j+1的值
                if (greater(a[j],a[j+1])){
                    exch(a,j,j+1);
                }
            }
        }
    }

    //比较元素v是否大于元素w
    private static boolean greater(Comparable v, Comparable w){
        return v.compareTo(w)>0;
    }

    //数组元素交换位置
    private static void exch(Comparable[] a, int i, int j){
        Comparable temp;
        temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }
}

冒泡排序时间复杂度分析：O（n^2）

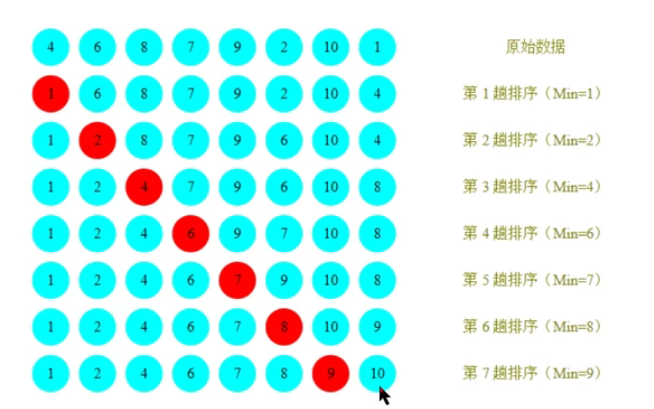
选择排序

排序原理：

1、每一次遍历过程中，都假定第一个索引处的元素是最小值，然后依次和其他索引处的值进行比较，直到找到本次遍历最小值

2、交换第一个索引处和最小值所在的索引处的值

image-20220117162148826

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
public class Selection {
    //对数组内的元素进行排序
    public static void sort(Comparable[] a){
        for (int i=0; i<=a.length-2; i++){
            //定义变量，记录最小索引所在位置，默认为每一次遍历的第一个元素
            int minIndex = i;
            for (int j=i+1; j<a.length; j++){
                //比较minIndex，与现在索引所在的值
                if (greater(a[minIndex],a[j])){
                    minIndex = j;
                }
            }

            //交换最小值和每次遍历的第一个值
            exch(a,i,minIndex);
        }
    }

    //比较元素v是否大于元素w
    private static boolean greater(Comparable v, Comparable w){
        return v.compareTo(w)>0;
    }

    //数组元素交换位置
    private static void exch(Comparable[] a, int i, int j){
        Comparable temp;
        temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }

}

选择排序时间复杂度分析：O（n^2）

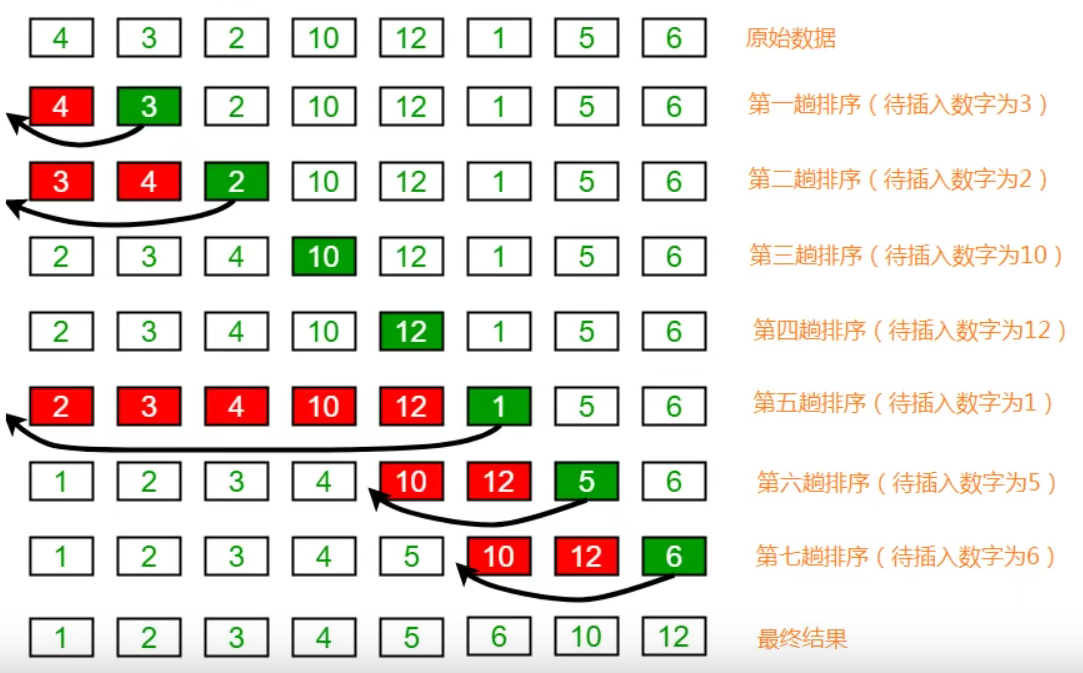
插入排序

排序原理：

1、将所有元素分为已排序和未排序

2、将未排序数组的第一个元素向已排序数组中插入

3、倒叙遍历已排序数组，找到小于或等于插入元素的元素，并将插入元素放到这个位置，其余元素向后移动一位

image-20220117183137041

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
public class Insertion {
    //对数组a中的元素进行排序
    public static void sort(Comparable[] a){
        for (int i =1; i<a.length; i++){
            for (int j=i; j>0; j--){
                //比较索引j处的值和索引j-1处的值
                //如果j-1处的值比j大则j--，小就交换
                if (greater(a[j-1],a[j])){
                    exch(a,j-1,j);
                }else {
                    break;
                }
            }
        }
    }

    //比较元素v是否大于元素w
    private static boolean greater(Comparable v, Comparable w){
        return v.compareTo(w)>0;
    }

    //数组元素交换位置
    private static void exch(Comparable[] a, int i, int j){
        Comparable temp;
        temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }
}

**插入排序时间复杂度分析：O（n^2） **

（其本质跟冒泡排序相似）

高级排序

希尔排序

希尔排序是插入排序的一种，又叫”缩小增量排序“，希尔排序的增量没有固定的规则

希尔排序的时间的时间复杂度为

img

，希尔排序时间复杂度的下界是n*log2n。希尔排序没有快速排序算法快 O(n(logn))，因此中等大小规模表现良好，对规模非常大的数据排序不是最优选择。但是比

img

复杂度的算法快得多。

专家们提倡，几乎任何排序工作在开始时都可以用希尔排序，若在实际使用中证明它不够快，再改成快速排序这样更高级的排序算法

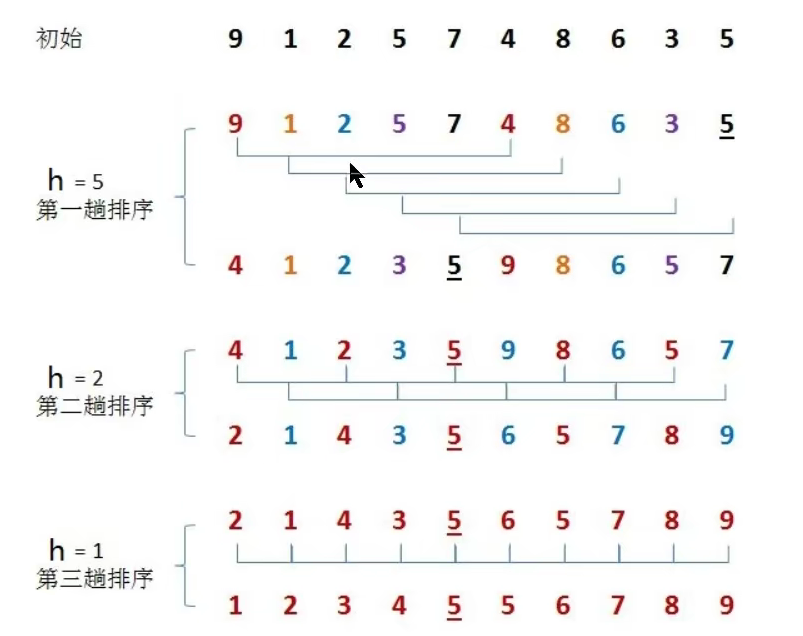
排序原理：

1、选定一个增量h，按照增量h作为数据分组的依据，对数据进行分组

2、对分好组的每一组数据完成插入排序

3、减小增长量，最小减一，重复第二步

image-20220117202712044

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
public class Shell {
    //对数组内的元素进行排序
    public static void sort(Comparable[] a){
        //根据数组的长度，确定增长量
        int h=1;
        while (h<a.length/2){
            h=2*h+1;
        }
        //希尔排序
        while (h>=1){
            //找待插入的元素
            //从h之后的每一个元素都需要进行跟自己的组进行排序，这是i++的原因
            for (int i=h; i<a.length; i++){
                //插入排序
                for (int j=i; j>=h; j-=h){
                    if (greater(a[j-1],a[j])){
                        exch(a,j-1,j);
                    }else {
                        break;
                    }
                }
            }
            //减小增长量
            h=h/2;
        }
    }

    //比较元素v是否大于元素w
    private static boolean greater(Comparable v, Comparable w){
        return v.compareTo(w)>0;
    }

    //数组元素交换位置
    private static void exch(Comparable[] a, int i, int j){
        Comparable temp;
        temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }
}

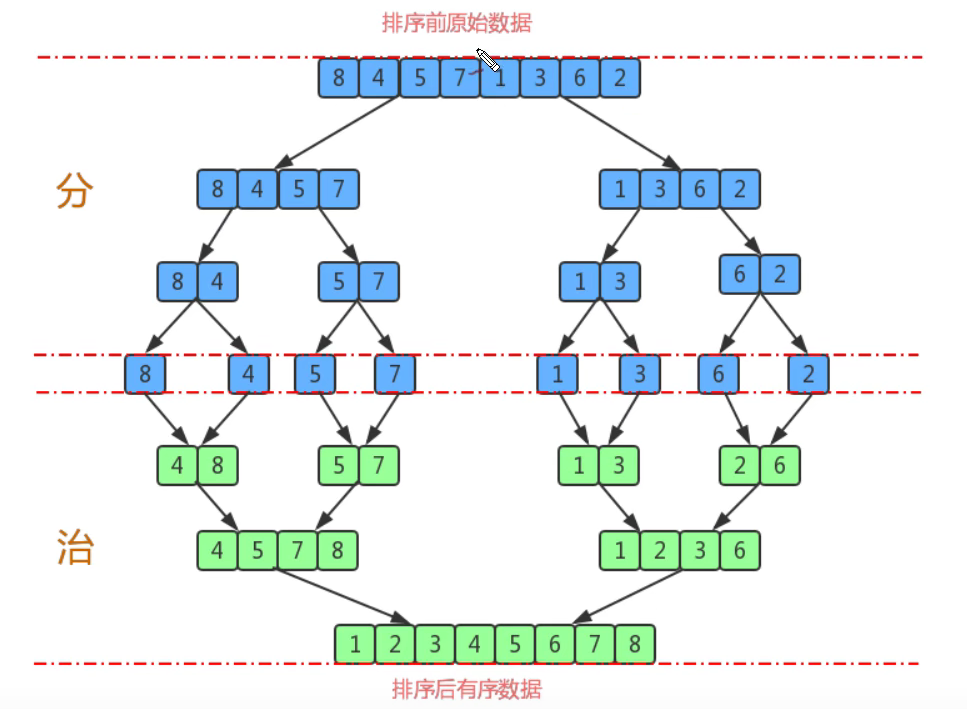
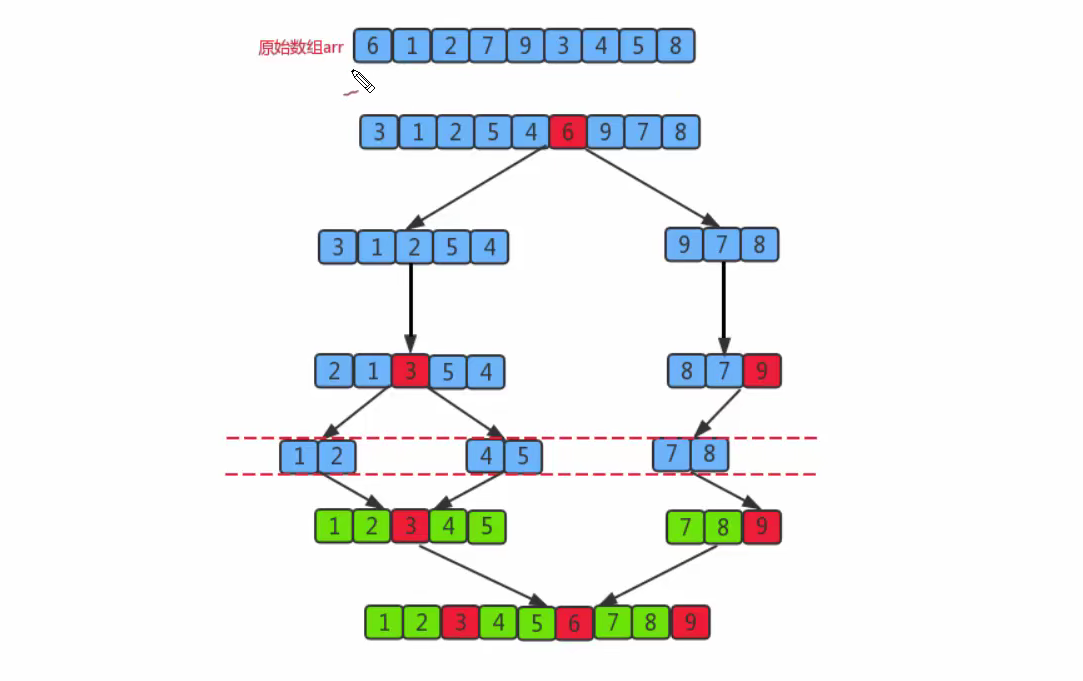
归并排序

归并排序体现的是分而治之的思想

排序原理：

1、尽可能的将一组数据拆分成两个元素相等的子组，并对每一个子组继续拆分，直到拆分后的每个子组的元素个数为1

2、不断将相邻的两个子组进行合并成一个有序的大组，直到只有一个组为止

image-20220117214230426

使用辅助数组，对两个子组进行排序，排序方式与合并两个有序链表的方式类似

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
public class Merge {
    //辅助数组
    private static Comparable[] assist;

    //对数组内的元素进行排序
    public static void sort(Comparable[] a){
        //初始化辅助数组
        assist = new Comparable[a.length];
        //定义一个lo变量和hi变量，分别记录数组中最小和最大的索引
        int lo = 0;
        int hi = a.length-1;
        //调用sort重载方法
        sort(a,lo,hi);
    }

    //对数组a中从索引lo到索引hi的元素进行排序
    private static void sort(Comparable[] a, int lo, int hi){
        //做安全性校验
        if (hi<=lo){
            return;
        }

        /**
         * 定义一个mid变量 将lo到hi之间的数据分成两组
         * sort(a,lo,mid);
         * sort(a,mid+1,hi);
         * 递归分组
         */
        int mid = lo+(hi-lo)/2;

        //分别对每一组数据进行排序
        sort(a,lo,mid);
        sort(a,mid+1,hi);

        //再把两个组中的数据进行合并
        merge(a,lo,mid,hi);
    }

    //将两个有序的子组合并成一个有序的大组
    private static void merge(Comparable[] a, int lo, int mid, int hi){
        //定义三个指针
        //辅助数组的指针
        int i = lo;

        int p1 = lo;
        int p2 = mid+1;

        //遍历，将两有序子组合并
        while (p1<=mid && p2<hi){
            if (less(a[p1],a[p2])){
                assist[i++] = a[p1++];
            }else {
                assist[i++] = a[p2++];
            }
        }

        //当其中某一个子组遍历完成，而另一个子组未完成时
        //将剩余元素顺序放入辅助数组中
        while (p1<=mid){
            assist[i++] = a[p1++];
        }

        while (p2<=hi){
            assist[i++] = a[p2++];
        }

        //将辅助数组中的元素拷贝到原数组的对应位置
        for (int index=lo; index<=hi; index++){
            a[index] = assist[index];
        }
    }

    //比较元素v是否小于元素w
    private static boolean less
    (Comparable v, Comparable w){
        return v.compareTo(w)<0;
    }

    //数组元素交换位置
    private static void exch(Comparable[] a, int i, int j){
        Comparable temp;
        temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }
}

归并排序的时间复杂度分析：O（n logn）

快速排序

排序原理：

1、首先设定一个分界值，通过该分界值将数组分成左右两部分

2、将大于或等于分界值的放到数组右边，小于分界值的放到数值左边

3、重复操作分界值左右两边的元素，最终就得到排序好的数组

image-20220118201405192

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
public class Quick {
    //对数组内的元素进行排序
    public static void sort(Comparable[] a){
        int lo = 0;
        int hi = a.length-1;
        sort(a,lo,hi);
    }

    //对数组a中从索引lo到索引hi的元素进行排序
    private static void sort(Comparable[] a, int lo, int hi){
        //安全性校验
        if (lo>=hi){
            return;
        }

        /**
         * 获得分界值的索引，分界值右边比分界值大，左边比分界值小
         * 并已分界值两边分为两组
         */
        int partition = partition(a,lo,hi);//返回的是分界值的索引，分界值位置变换后的索引

        //使左子组有序
        sort(a,lo,partition-1);

        //使右子组有序
        sort(a,partition+1,hi);
    }

    /**
     * 这个方法的作用是使用分界值（默认为数组第一个元素）对数组lo到hi的元素进行分组
     * 比分界值大的放右边，比分界值小的放左边
     * @return 返回分组之后分界值所在的索引（因为分界值一开始的索引为lo，所以最后分界值的位置会发生变化）
     */
    private static int partition(Comparable[] a, int lo, int hi){
        //确定分界值
        Comparable key = a[lo];
        //定义两个指针，分别指向待切分元素的最小索引和最大索引的下个位置
        int left = lo;
        int right = hi+1;

        //切分
        while(true){
            //先从右往左扫描，找到一个比分界值小的元素然后停止
            while (less(key,a[--right])){
                if (right == lo){
                    break;
                }
            }
            //先从左往右扫描，找到一个比分界值大的元素然后停止
            while (less(a[++left],key)){
                if (left == hi){
                    break;
                }
            }
            //循环结束
            if (left>=right){
                break;
            }else {
                exch(a,left,right);
            }
        }

        //交换right与分界值，此处不能与left交换，因为left可能大于right，若与letf交换可能会导致，比分界值大的被交换
        exch(a,lo,right);

        return  right;
    }

    //比较元素v是否小于元素w
    private static boolean less
    (Comparable v, Comparable w){
        return v.compareTo(w)<0;
    }

    //数组元素交换位置
    private static void exch(Comparable[] a, int i, int j){
        Comparable temp;
        temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }
}

快速排序的时间复杂度分析：最优情况：O（nlogn） 最坏情况：O（n^2）

归并排序和快速排序的区别：

归并排序将数组分成两个子数组分别排序，并将有序的子数组归并，从而将整个数组排序

快速排序的方式是当两个数组都有序时，整个数组就有序了

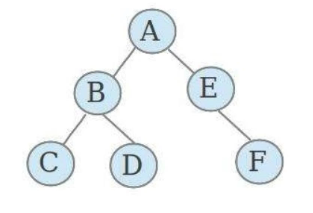
树

树的定义：

树是由n个有限结点组成一个具有层次关系的集合。它看起来像一颗倒挂的树

树的特点：

1、每个结点有零个或多个子结点

2、没有父节点的结点为根结点

3、每一个非根节点只有一个父结点

4、每个结点及其后代结点整体上可以看作是一个棵树，称为当前结点的父节点的一个子树

结点的度：

一个结点含有的子树的个数称为该结点的度

叶结点：

度为0的结点也称为叶结点

树的度：

树中所有结点的度的最大值

树的深度：

树中结点的最大层次

二叉树

二叉树就是度不超过2的树

image-20220119200839620

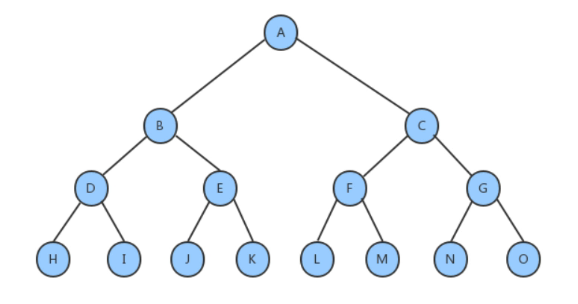
满二叉树：

一个二叉树，如果每一个层的结点树都达到最大值，则这个二叉树就是满二叉树

image-20220119201015460

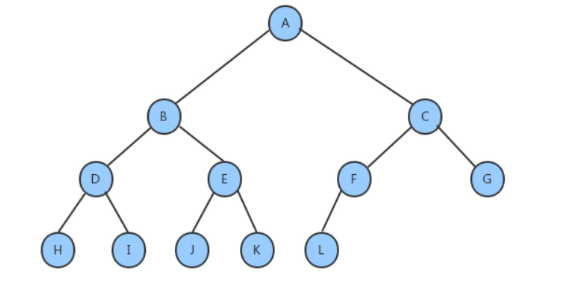
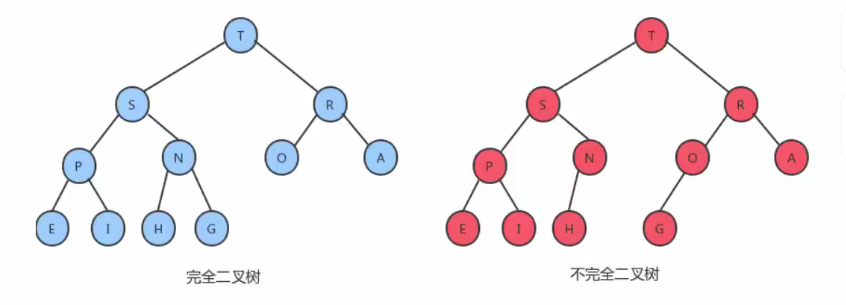
完全二叉树：

叶结点只能出现在最下层和次下层

image-20220119201231459

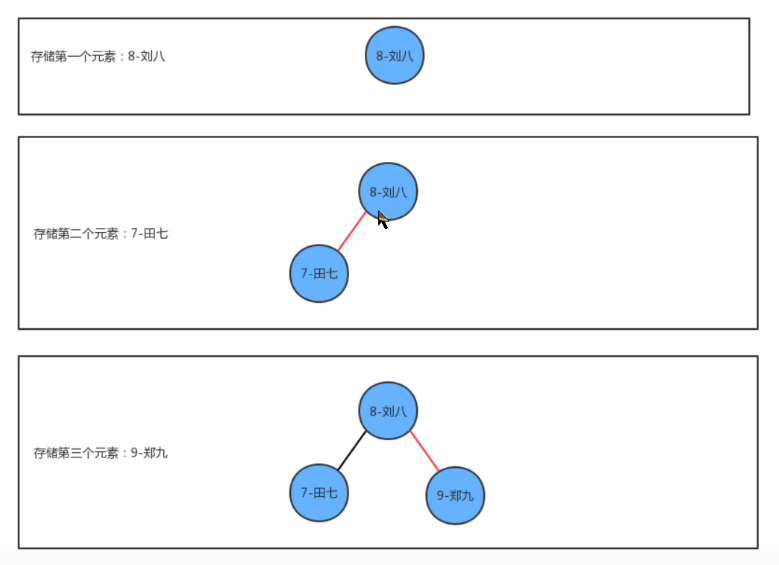
二叉查找树的创建

插入方法put的实现思想：

1、如果当树中没有任何一个结点，则直接把新结点作为根结点

2、如果当前树不为空，则从根结点开始

  • 如果新结点的key小于当前结点的key，则继续找当前结点的左子结点
  • 如果新结点的key大于当前结点的key，则继续找当前结点的右子结点
  • 如果新结点的key等于当前结点的key，则树中已经存在这样的结点，替换该结点的value值即可

image-20220120141818232

查询方法get实现思想：

从根结点开始

  • 如果要查询的key小于当前结点的key，则继续找当前结点的左子结点
  • 如果要查询的key大于当前结点的key，则继续找当前结点的右子结点
  • 如果要查询的key等于当前结点的key，则返回当前结点的value值

删除方法delete实现思想：

  • 找到被删除结点

  • 找到被删除结点右子树的最小结点minNode

  • 删除右子树中的最小结点

  • 让被删除结点的左子树成为最小结点minNode的左子树，让被删除结点的右子树成为最小结点minNode的右子树

  • 让被删除结点的父结点指向最小结点minNode

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
public class BinaryTree <Key extends Comparable<Key>,Value>{
    private Node root; //记录根结点
    private int N; //记录树中元素的个数

    //向树中插入一个键值对
    public void put(Key key, Value value){
        root = put(root,key,value);
    }

    //给指定树x上，添加一个键值对，并返回添加后的新树
    public Node put(Node x, Key key, Value value){
        //如果x子树为null
        if (x == null){
            N++;
            return new Node(key,value,null,null);
        }

        //如果x子树不为null
        //比较x结点的键和key的大小
        int cmp = key.compareTo((Key) x.key);

        if (cmp>0){
            //key > x.key，继续找右子树
            x.right = put(x.right,key,value);
        }else if (cmp<0){
            //key < x.key，继续找左子树
            x.left = put(x.left,key,value);
        }else {
            //key = x.key，替换x的value
            x.value = value;
        }

        return x;
    }

    //根据key，从树中找出对应的值
    public Value get(Key key){
        return get(root,key);
    }

    //从指定的树x中，找出key对应的值
    private Value get(Node x, Key key){
        //如果x子树为null
        //包含了找不到key值的情况
        if (x == null){
            return null;
        }

        //如果x子树不为null
        //比较x结点的键和key的大小
        int cmp = key.compareTo((Key) x.key);

        if (cmp>0){
            //key > x.key，继续找右子树
            return get(x.right,key);
        }else if (cmp<0){
            //key < x.key，继续找左子树
            return get(x.left,key);
        }else {
            //key = x.key，返回x的value
            return (Value) x.value;
        }

    }

    //根据key，删除树中对应的键值对
    public void delete(Key key){
        delete(root,key);
    }

    //删除指定树x上的键为key的键值对，并返回删除后的新树
    public Node delete(Node x, Key key){
        //如果x子树为null
        //包含了找不到key值的情况
        if (x == null){
            return null;
        }

        //如果x子树不为null
        //比较x结点的键和key的大小
        int cmp = key.compareTo((Key) x.key);

        if (cmp>0){
            //key > x.key，继续找右子树
            x.right = delete(x.right,key);
        }else if (cmp<0){
            //key < x.key，继续找左子树
            x.left = delete(x.left,key);
        }else {
            //key = x.key，执行删除操作

            //找到右子树中最小的结点
            if (x.right == null){
                return x.left;
            }
            if (x.left == null){
                return x.right;
            }
            Node minNode = x.right;
            while (minNode.left != null){
                minNode = minNode.left;
            }

            //找到并删除右子树中最小的结点
            Node n = x.right;
            while (n.left != null){
                if (n.left.left == null){
                    n.left = null;
                }else {
                    //变换n结点
                    n = n.left;
                }
            }

            //让x结点的左子树成为minNode的左子树
            minNode.left = x.left;

            //让x结点的右子树成为minNode的右子树
            minNode.right = x.right;

            //让x结点的父结点指向minNode
            x = minNode;

            //元素个数减一
            N--;
        }

        return x;
    }

    //获取树中元素的个数
    public int size(){
        return N;
    }
}
二叉查找树中最小的键
1
2
3
4
5
6
7
8
9
10
11
12
//返回二叉查找树中最小的键
public Key min(){
    return (Key) min(root).key;
}

public Node min(Node x){
    if (x.left != null){
        return min(x.left);
    }else {
        return x;
    }
}
二叉查找树中最大的键
1
2
3
4
5
6
7
8
9
10
11
12
//返回二叉查找树中最大的键
public Key max(){
    return (Key) min(root).key;
}

public Node max(Node x){
    if (x.right != null){
        return max(x.right);
    }else {
        return x;
    }
}
二叉树的遍历

很多情况下，我们需要遍历树，由于树状结构和线性结构不一样，它没有办法从头开始依次向后遍历，所以存在如何遍历，也就是按照什么样的搜索路径进行遍历的问题

我们可以把二叉树的低级遍历方式分为以下三种方式：

1、先序遍历：

先访问根结点，再访问左子树，最后访问右子树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
//使用先序遍历，获取整个树中的所有键
public List<Key> preErgodic(){
    List<Key> keys = new ArrayList<>();
    preErgodic(root,keys);
    return keys;
}

private void preErgodic(Node x, List<Key> keys){
    if (x == null){
        return;
    }

    //将x.key放入keys
    keys.add((Key) x.key);

    //判断左右子树是否为null
    if (x.left != null){
        preErgodic(x.left,keys);
    }
    if (x.right != null){
        preErgodic(x.right,keys);
    }
}

2、中序遍历：

先访问左子树，再访问根结点，最后访问右子树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
//使用中序遍历，获取整个树中的所有键
public List<Key> midErgodic(){
    List<Key> keys = new ArrayList<>();
    midErgodic(root,keys);
    return keys;
}

private void midErgodic(Node x, List<Key> keys){
    if (x == null){
        return;
    }

    //判断左右子树是否为null
    if (x.left != null){
        midErgodic(x.left,keys);
    }

    //将x.key放入keys
    keys.add((Key) x.key);

    if (x.right != null){
        midErgodic(x.right,keys);
    }
}

3、后序遍历：

先访问左子树，再访问右子树，最后访问根结点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
//使用后序遍历，获取整个树中的所有键
public List<Key> afterErgodic(){
    List<Key> keys = new ArrayList<>();
    afterErgodic(root,keys);
    return keys;
}

private void afterErgodic(Node x, List<Key> keys){
    if (x == null){
        return;
    }

    //判断左右子树是否为null
    if (x.left != null){
        afterErgodic(x.left,keys);
    }
    if (x.right != null){
        afterErgodic(x.right,keys);
    }


    //将x.key放入keys
    keys.add((Key) x.key);

}

高级遍历方式：层序遍历

实现步骤：

  • 创建队列，存储每一层的结点

  • 使用循环从队列弹出一个结点

    • 获取当前结点的key

    • 如果当前结点的左子结点不为空，则把左子结点放入到队列中

    • 如果当前结点的右子结点不为空，则把右子结点放入到队列中

此处使用ArrayList来代替队列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
//层序遍历
    public List<Key> layerErgodic(){
        List<Key> keys = new ArrayList<>();
        List<Node> nodes = new ArrayList<>();

        //默认往队列中放入根结点
        nodes.add(root);

        while (!nodes.isEmpty()){
            //从队列中弹出结点，把key放入keys中
            Node node = nodes.get(0);
            nodes.remove(0);
            keys.add((Key) node.key);

            //判断当前结点是否有左子结点，有则放入nodes中
            if (node.left != null){
                nodes.add(node.left);
            }

            //判断当前结点是否有右子结点，有则放入nodes中
            if (node.right != null){
                nodes.add(node.right);
            }
        }
        return keys;
    }
二叉树的最大深度问题

给定一颗树，计算树的最大深度（树的根结点到最远叶子结点的最长路径上的结点数）

实现步骤：

  • 如果根结点为空，则最大深度为0
  • 计算左子树的最大深度
  • 计算右子树的最大深度
  • 当前树的最大深度 = 左子树的最大深度和右子树的最大深度中的较大者 + 1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
//计算指定的树的最大深度
    public int maxDepth(Node x){
        if (x == null){
            return 0;
        }

        //x的最大深度
        int max = 0;
        //左子树的最大深度
        int maxL = 0;
        //右子树的最大深度
        int maxR = 0;

        //计算左子树最大深度
        if (x.left != null){
            maxL = maxDepth(x.left);
        }

        //计算右子树最大深度
        if (x.right != null){
            maxR = maxDepth(x.right);
        }

        //比较左右子树最大深度，取较大值+1
        max = maxL>maxR?maxL+1:maxR+1;

        return max;
    }

堆

堆的定义

堆是计算机科学中一类特殊的数据结构的统称，堆通常可以被看做是一颗完全二叉树的数组对象

堆的特性：

1、它是完全二叉树，除了树的最后一层结点不需要是满的，其它的每一层从左到右都是满的，如果最后一层不满，则要求左满右不满

image-20220123162158170

2、它通常是用数组来实现

具体方法就是将二叉树的结点按照层级顺序放入数组中

如果一个结点为位置为k，则它的父结点则为【k/2】，而它的两个子结点的位置则分别为【2k】和【2k+1】

3、每个结点都大于等于它的两个子结点。虽然这样规定，但是子结点的位置顺序并没有规定

堆的实现

insert插入方法的实现

由于堆的定义是父结点大于两个子结点，且堆是由数组实现，所以在我们插入一个比父结点大的元素时就需要从插入元素的位置不断跟其父结点比较，如果父结点比子结点小则交换位置

delMax删除最大元素方法的实现

由于堆的定义，其根结点就是最大值，所以将其删除后将会导致堆的顺序变化，从而导致堆不符合定义；所以这时我们可以暂时把堆中最后一个元素拿出，并放到索引1处，然后使用下沉算法使堆有序

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
public class Heap<T extends Comparable> {
    private T[] items; //用来存储元素的数组
    private int N; //记录堆中元素的个数

    //创建容量为capacity的Heap对象
    public Heap(int capacity){
        this.items = (T[])new Comparable[capacity+1];
        this.N = 0;
    }

    //判断堆中索引i处的元素是否小于索引j处的元素
    private boolean less(int i, int j){
        return items[i].compareTo(items[j])<0;
    }

    //交换堆中i索引和j索引处的值
    private void exch(int i, int j){
        T temp = items[i];
        items[i] = items[j];
        items[j] = temp;
    }

    //删除堆中最大的元素，并返回这个最大元素
    public T delMax(){
        T max = items[1];

        //交换索引1处的元素和最大索引处的元素
        exch(1,N);

        //删除最大索引元素
        items[N] = null;

        //元素个数减一
        N--;

        //让堆有序
        sink(1);
        return max;
    }

    //往堆中插入一个元素
    public void insert(T t){
        //索引0不使用
        items[++N] = t;
        //使用上浮算法，使堆有序
        swim(N);
    }


    //使用上浮算法，使索引k处的元素能在堆中处于一个正确的位置
    private void swim(int k){
        //不断比较当前结点和父结点的大小，如果父结点比子结点小，则交换位置
        while (k>1){
            //比较当前结点和父结点的值
            if (less(k/2,k)){
                exch(k/2,k);
            }
            k=k/2;
        }
    }

    //使用下沉算法，使索引k处的元素能在堆中处于一个正确的位置
    private void sink(int k){
        //不断对比当前k结点和其子结点的较大值，如果当前结点小于子节点较大值，则交换位置
        while (2*k <= N){
            //获取当前结点的较大结点
            int max; //记录较大结点所在的索引
            if(2*k+1 < N){
                if (less(2*k,2*k+1)){
                    max = 2*k+1;
                }else {
                    max = 2*k;
                }
            }else {
                max = 2*k;
            }

            //比较当前结点和较大子结点的值
            if (!less(k,max)){
                break;
            }

            //交换值
            exch(k,max);

            //变换k值
            k = max;
        }

    }
}

堆排序

实现步骤：

1、构造堆

2、得到堆顶元素

3、交换堆顶元素和数组中的最后一个元素，此时所有元素中的最大元素已经放到合适的位置

4、对堆进行调整，重新让除了最后一个元素的剩余元素中的最大值放到堆顶

5、重复2~4步骤，直到堆中剩余一个元素为止

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
public class HeapSort {
    //对source数组中的数据从小到大排序
    public static void sort(Comparable[] source){
        //构建堆
        Comparable[] heap = new Comparable[source.length+1];
        createHeap(source,heap);

        //定义一个变量，记录未排序的元素中最大的索引
        int N = heap.length-1;

        //通过循环，交换1索引处的元素和排序的元素中最大索引处的值
        while (N != 1){
            //交换元素
            exch(heap,1,N);
            //排序交换后最大元素所在的索引让其不再参加堆的下沉调整
            N--;
            //需要对索引1处的元素进行堆的下沉调整
            sink(heap,1,N);
        }
        //把heap中数据复制到原数组source
        System.arraycopy(heap,1,source,0,source.length);

    }

    //根据原数组source，构造出heap
    private static void createHeap(Comparable[] source, Comparable[] heap){
        //把source中的元素拷贝到heap中，heap中的元素就形成一个无序的堆
        System.arraycopy(source,0,heap,1,source.length);
        //对堆中的元素做下沉调整（从长度的一半处开始，往索引1处扫描）
        for (int i = (heap.length)/2; i>0; i--){
            sink(heap,i,heap.length-1);
        }
    }

    //判断heap堆中索引i处的元素是否小于索引j处的元素
    private static boolean less(Comparable[] heap, int i, int j){
        return heap[i].compareTo(heap[j]) < 0;
    }

    //交换heap中i索引和j索引处的值
    private static void exch(Comparable[] heap, int i, int j){
        Comparable temp = heap[i];
        heap[i] = heap[j];
        heap[j] = temp;
    }

    //在heap中，对target处的元素做下沉，范围是0~range
    private static void sink(Comparable[] heap, int target, int range){
        while (2*target<=range){
            //1、找出当前结点的较大子结点
            int max;
            if (2*target+1<range){
                if (less(heap,2*target,2*target+1)){
                    max = 2*target+1;
                }else {
                    max = 2*target;
                }
            }else {
                max = 2*target;
            }

            //2、比较当前结点的值和较大子结点的值
            if (!less(heap,target,max)){
                break;
            }
            exch(heap,target,max);
            target = max;
        }
    }
}